研究设计与统计

订阅

MedSci主页 / 所有栏目 / 研究设计与统计

SPSS教程第十五课：生存分析

2012-04-12 生物谷 生物谷

SPSS教程统计
关注

 在临床诊疗工作的评价中，慢性疾病的预后一般不适合用治愈率、病死率等指标来考核，因为其无法在短时间内明确判断预后情况，为此，只能对患者进行长期随访，统计一定时期后的生存或死亡情况以判断诊疗效果。这就是生存分析。   第一节 Life Tables过程   14.1.1 主要功能     调用此过程时，系统将采用即寿命表分析法，完

 在临床诊疗工作的评价中，慢性疾病的预后一般不适合用治愈率、病死率等指标来考核，因为其无法在短时间内明确判断预后情况，为此，只能对患者进行长期随访，统计一定时期后的生存或死亡情况以判断诊疗效果。这就是生存分析。

 

第一节 Life Tables过程

 

14.1.1 主要功能

    调用此过程时，系统将采用即寿命表分析法，完成对病例随访资料在任意指定时点的生存状况评价。

 

14.1.2 实例操作

   ［例14-1］ 用中药+化疗（中药组，16例）和单纯化疗（对照组，10例）两种疗法治疗白血病患者后，随访记录存活情况如下所示，试比较两组的生存率。

 

中药组

对照组

随访月数

是否死亡

随访月数

是否死亡

10

2

12

13

18

6

19

26

9

8

6

43

9

4

31

24

否

是

是

否

否

是

是

否

是

是

是

是

否

否

否

否

2

13

7

11

6

1

11

3

17

7

是

否

是

是

否

否

否

否

否

否

 

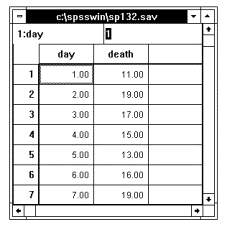
14.1.2.1  数据准备

    激活数据管理窗口，定义变量名：随访月数的变量名为TIME，是否死亡的变量名为DEATH，分组（即中药组与对照组）的变量名为GROUP。输入原始数据：随访月数按原数值；是否死亡的，是为1，否为0；分组的，中药组为1，对照组为2。

 

14.1.2.2  统计分析

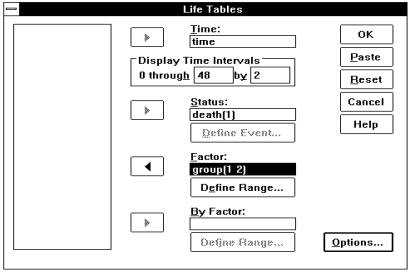
    激活Statistics菜单选Survival中的Life Tables...项，弹出Life Tables对话框（图14.1）。从对话框左侧的变量列表中选time，点击Ø钮使之进入time框；在Display Time Intervals栏中定义需要显示生存率的时点，本例要求从0个月显示至48个月，间隔为2个月，故在0 through框中输入48，在by框中输入2。选death，点击Ø钮使之进入Status框，点击Define Event...钮弹出Life Tables:Define Event for Status Variable对话框，在Single value栏中输入1，表明death = 1为发生死亡事件者；点击Continue钮返回Life Tables对话框。选group，点击Ø钮使之进入Factor框，点击Define Range...钮，弹出Life Tables:Define Range for Factor Variable对话框，定义分组的范围，在Mininum框中输入1，在Maxinum框中输入2，点击Continue钮返回Life Tables对话框。

 

图14.1  生存资料的寿命表分析对话框 

       点击Options...钮弹出Life Tables: Options对话框，在Plot栏中选Survival项，要求绘制生存率曲线图；在Compare Levels of First Factor栏中选Overall项，要求作组间生存状况的比较。之后点击Continue钮返回Life Tables对话框，再点击OK钮即完成分析。

 

14.1.2.3  结果解释

       在结果输出窗口中将看到如下统计数据：

       共有26个观察对象进入分析。系统先显示中药组（group = 1）的生存状况寿命表，按用户指定，从0月起，隔2个月直至42个月（原指定从0—48个月，但因42个月后，生存概率已为0，故42个月后至48个月的生存状况不再显示），分别显示进入该时点例数（Number Entrng this Intrvl）、从该时点失去的例数（Number Wdrawn Durong Intrvl）、该时点暴露于死亡危险的例数（Number Exposd to Risk）、该时点死亡的例数（Number of Termnl Events）、该时点死亡概率（Propn Terminating）、该时点生存概率（Propn Surviving）、该时点末生存率（Propn Surv at End）、单位时点的累积概率（Cumul Probability Densty）、该时点风险比例（Hazard Rate）、生存率的标准误（SE of Cumul Surviving）、单位时点累积概率的标准误（SE of Probability Densty）、风险比例的标准误（SE of Hazard Rate）。如本例，用中药+化疗的方式治疗白血病患者，至8个月时，死亡率为17.39%，生存概率为82.61%，生存率为66.38%，风险比例为9.52%。至42个月时，生存概率和生存率均为0，此时风险比例为100%。中药组的50%生存率在19.44个月。

       对照组同类结果的显示，因在16个月时生存概率已为0，故仅从0月起，隔2个月至16个月止。分析显示，单纯用化疗，白血病患者的半数生存率约在16个月多一点，比中药组少三个月。

 

This subfile contains:      26 observations

 

 Life Table

   Survival Variable  TIME

                 for  GROUP =  1

    Number Number Number Number                   Cumul        SE of  SE of

Intrvl Entrng Wdrawn Exposd   of    Propn  Propn Propn  Proba-       Cumul  Proba-  SE of

Start  this   During   to   Termnl  Termi-  Sur-  Surv   bility  Hazard  Sur-  bility   Hazard

Time  Intrvl  Intrvl   Risk  Events  nating  viving  at End Densty  Rate  viving  Densty   Rate

------  ------  ------   ------  ------   ------   ------  ------  ------   ------  ------   ------   ------

  .0   16.0    .0    16.0    .0    .0000  1.0000 1.0000  .0000  .0000  .0000  .0000   .0000

 2.0   16.0    .0    16.0   1.0    .0625   .9375  .9375  .0313  .0323  .0605  .0303   .0322

 4.0   15.0   1.0    14.5    .0    .0000  1.0000  .9375  .0000  .0000  .0605  .0000   .0000

 6.0   14.0    .0    14.0   2.0    .1429   .8571  .8036  .0670  .0769  .1019  .0441   .0542

 8.0   12.0   1.0    11.5   2.0    .1739   .8261  .6638  .0699  .0952  .1231  .0458   .0670

10.0    9.0   1.0     8.5    .0    .0000  1.0000  .6638  .0000  .0000  .1231  .0000   .0000

12.0    8.0   1.0     7.5   1.0    .1333   .8667  .5753  .0443  .0714  .1348  .0420   .0712

14.0    6.0    .0     6.0    .0    .0000  1.0000  .5753  .0000  .0000  .1348  .0000   .0000

16.0    6.0    .0     6.0    .0    .0000  1.0000  .5753  .0000  .0000  .1348  .0000   .0000

18.0    6.0   1.0     5.5   1.0    .1818   .8182  .4707  .0523  .1000  .1453  .0489   .0995

20.0    4.0    .0     4.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

22.0    4.0    .0     4.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

24.0    4.0   1.0     3.5    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

26.0    3.0   1.0     2.5    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

28.0    2.0    .0     2.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

30.0    2.0   1.0     1.5    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

32.0    1.0    .0     1.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

34.0    1.0    .0     1.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

36.0    1.0    .0     1.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

38.0    1.0    .0     1.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

40.0    1.0    .0     1.0    .0    .0000  1.0000  .4707  .0000  .0000  .1453  .0000   .0000

42.0    1.0    .0     1.0   1.0   1.0000   .0000  .0000  .2354 1.0000   .0000  .0727   .0000

 

 The median survival time for these data is  19.44

 

Life Table

   Survival Variable  TIME

                 for  GROUP =  2

    Number Number Number Number                   Cumul        SE of  SE of

Intrvl Entrng Wdrawn Exposd   of    Propn  Propn Propn  Proba-       Cumul  Proba-  SE of

Start  this   During   to   Termnl  Termi-  Sur-  Surv   bility  Hazard  Sur-  bility   Hazard

Time  Intrvl  Intrvl   Risk  Events  nating  viving  at End Densty  Rate  viving  Densty   Rate

------  ------  ------   ------  ------   ------   ------  ------  ------   ------  ------   ------   ------

  .0   10.0   1.0     9.5    .0    .0000  1.0000 1.0000  .0000  .0000  .0000  .0000   .0000

 2.0    9.0   1.0     8.5   1.0    .1176   .8824  .8824  .0588  .0625  .1105  .0553   .0624

 4.0    7.0    .0     7.0    .0    .0000  1.0000  .8824  .0000  .0000  .1105  .0000   .0000

 6.0    7.0   2.0     6.0   1.0    .1667   .8333  .7353  .0735  .0909  .1628  .0678   .0905

 8.0    4.0    .0     4.0    .0    .0000  1.0000  .7353  .0000  .0000  .1628  .0000   .0000

10.0    4.0   1.0     3.5   1.0    .2857   .7143  .5252  .1050  .1667  .2122  .0918   .1643

12.0    2.0   1.0     1.5    .0    .0000  1.0000  .5252  .0000  .0000  .2122  .0000   .0000

14.0    1.0    .0     1.0    .0    .0000  1.0000  .5252  .0000  .0000  .2122  .0000   .0000

16.0    1.0   1.0      .5    .0    .0000  1.0000  .5252  .0000  .0000  .2122  .0000   .0000

 

 The median survival time for these data is  16.00+

 

 

       接着显示两组比较的结果。系统采用Gehan比分检验法，得u = 0.012，P = 0.9113，即中药组与对照组的生存率无差别。

 

版权声明：
本网站所有内容来源注明为“williamhill asia 医学”或“MedSci原创”的文字、图片和音视频资料，版权均属于williamhill asia 医学所有。非经授权，任何媒体、网站或个人不得转载，授权转载时须注明来源为“williamhill asia 医学”。其它来源的文章系转载文章，或“williamhill asia 号”自媒体发布的文章，仅系出于传递更多信息之目的，本站仅负责审核内容合规，其内容不代表本站立场，本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与williamhill asia 联系，williamhill asia 将立即进行删除处理。
在此留言
评论区 (1)
#插入话题
  1. [GetPortalCommentsPageByObjectIdResponse(id=52227, encodeId=2cf15222eea, content=不错，但是没有看到我想要的，很想治疗如何计算累积死亡率及曲线, beContent=null, objectType=article, channel=null, level=null, likeNumber=112, replyNumber=0, topicName=null, topicId=null, topicList=[], attachment=null, authenticateStatus=null, createdAvatar=, createdBy=b1af1671926, createdName=颜, createdTime=Tue Jan 05 20:49:00 CST 2016, time=2016-01-05, status=1, ipAttribution=)]
    2016-01-05 颜

    不错，但是没有看到我想要的，很想治疗如何计算累积死亡率及曲线

    0

相关威廉亚洲官网

SPSS教程第九课：回归分析

 回归分析是处理两个及两个以上变量间线性依存关系的统计方法。在医学领域中，此类问题很普遍，如人头发中某种金属元素的含量与血液中该元素的含量有关系，人的体表面积与身高、体重有关系；等等。回归分析就是用于说明这种依存变化的数学关系。   第一节 Linear过程  8.1.1 主要功能     调用此过程可完成二元或多元的线性回归分析

SPSS教程第十三课：可靠性分析

2.1  主要功能     在精神卫生与社会医学研究中，经常需要借助量表来了解对象的某一特性。如常用的症状自评量表（SCL-90）即用于评定对象精神病症状的表现形式与强度；又如生活事件量表（LES）即用于对精神刺激进行定性和定量分析。在完成一份量表的编制工作后，或在准备将一份已有的量表作实际应用前，需要对量表的信度进行考核。   &

SPSS教程第十课：对数线性模型

对数线性模型是用于离散型数据或整理成列联表格式的计数资料的统计分析工具。在对数线性模型中，所有用作的分类的因素均为独立变量，列联表各单元中的例数为应变量。对于列联表资料，通常作χ2 检验，但χ2 检验无法系统地评价变量间的联系，也无法估计变量间相互作用的大小，而对数线性模型是处理这些问题的最佳方法。   第一节 General过程   9.1.1 主要功能  

SPSS教程第十一课：分类分析

人们认识事物时往往先把被认识的对象进行分类，以便寻找其中同与不同的特征，因而分类学是人们认识世界的基础科学。在医学实践中也经常需要做分类的工作，如根据病人的一系列症状、体征和生化检查的结果，判断病人所患疾病的类型；或对一系列检查方法及其结果，将之划分成某几种方法适合用于甲类病的检查，另几种方法适合用于乙类病的检查；等等。统计学中常用的分类统计方法主要是聚类分析与判别分析。  &nbs

SPSS教程第十四课：非参数检验

  许多统计分析方法的应用对总体有特殊的要求，如t检验要求总体符合正态分布，F检验要求误差呈正态分布且各组方差整齐，等等。这些方法常用来估计或检验总体参数，统称为参数统计。     但许多调查或实验所得的科研数据，其总体分布未知或无法确定，这时做统计分析常常不是针对总体参数，而是针对总体的某些一般性假设（如总体分布），这类方法称非参数统计（Nonparam

SPSS教程第十二课：因子分析

1  主要功能     多元分析处理的是多指标的问题。由于指标太多，使得分析的复杂性增加。观察指标的增加本来是为了使研究过程趋于完整，但反过来说，为使研究结果清晰明了而一味增加观察指标又让人陷入混乱不清。由于在实际工作中，指标间经常具备一定的相关性，故人们希望用较少的指标代替原来较多的指标，但依然能反映原有的全部信息，于是就产生了主成分分析、对应分析、典