时间-事件结局证据合成中时间的效应修饰作用

在涉及疾病痊愈、复发、死亡等重大问题上，研究者不仅关注事件是否发生，也关注事件发生的时间[1]。时间-事件（time-to-event）结局数据，亦称生存资料，是纵向研究中记录和描述事件发生状况及时间的数据类型，特别是在涉及心血管疾病、肿瘤的药物研究中较为常见。在对生存资料进行分析时，传统的多因素分析方法无法同时处理生存结局和生存时间，也不能充分利用删失时间所提供的不完全信息，具有半参数性质、严格依赖比例风险（proportional hazards，PH）假设的Cox比例风险回归模型成为了广为使用的分析方法[2]。然而，生存资料中可能存在时间的效应修饰（effect modification）作用，预后因素（如研究药物）对时间-事件结局的影响可能随着时间的变化而变化[3]。在2009年一项比较吉非替尼、卡铂联合紫杉醇治疗肺腺癌的随机对照试验中，就观察到了两组药物间无进展生存时间的Kaplan-Meier生存曲线交叉的情况，提示治疗效应存在时间依存性[4]。在此情况下，使用Cox比例风险回归模型，结果的准确性和可解释性将受到影响，错误的结果也将进一步影响临床决策及患者健康。在时间-事件结局的证据合成中，搜集、汇总随机对照试验中的生存资料进行Meta分析被公认是评价医疗干预措施效果的最佳证据[5]。传统的Meta分析直接使用纳入研究报告的结果，即研究水平上的集合数据（aggregate data）进行效应合并。这种分析方法受原始研究数据报告质量的限制，难以处理生存资料中时间的效应修饰作用[6]。本文首先介绍了时间-事件结局的概念及其常见统计分析方法，在此基础上以课题组既往发表的一篇钠-葡萄糖共转运蛋白2（sodium-glucose cotransporter-2，SGLT2）抑制剂在慢性心力衰竭中疗效及安全性的系统评价与Meta分析数据为例[7]，列举了当时间-事件结局中存在时间效应修饰作用时的处理方法，并进一步阐述了如何在时间-事件结局证据合成中使用规范的方法评估时间的效应修饰作用，以期为研究者提供参考依据。所有数据分析均使用R软件进行。

1   时间-事件结局

时间-事件结局是预后研究中的重要结局类型，这一结局信息不仅包括研究对象是否发生事件（event），也包含其发生事件的时间。时间-事件结局中的时间，通常指随访开始至研究对象发生目标事件的时间，可称为生存时间（survival time）。时间-事件结局中的事件，可以是死亡、疾病进展、缓解后复发，亦可以是其他研究关注的目标事件。在时间-事件结局中，还有删失（censoring）这一值得注意的情况。删失指的是研究中不能获得研究对象准确生存时间的情况，依据准确生存时间与观察时间的关系，可分为右删失（right-censored）、左删失（left-censored）以及区间删失（interval censored），临床研究中的删失多为右删失。通常情况下，临床研究基于一定的随访时间开展，当随访结束时仍未观察到研究对象发生目标事件，则其日后发生目标事件的准确时间也未知，此时研究对象即发生删失。当随访过程中研究对象出现失访或退出研究时，也不能获取其准确的生存时间。上述情况中，研究对象准确的生存时间等于最后观察时间或位于最后观察时间之后的情况统称为右删失。而当未知的准确生存时间发生在观察时间之前时称为左删失，在某一段时间范围内时称之为区间删失[8]。

2   时间-事件结局的常见分析方法

2.1   Kaplan-Meier方法

Kaplan与Meier在1958年合作提出了用于处理不完整观察数据的Kaplan-Meier方法[9]，此后这一非参数方法便广泛运用于估计时间-事件结局的生存概率（survival probability），Kaplan-Meier生存曲线也成为了预后研究中经典的结局呈现形式。该方法将研究中研究对象所在组别、发生事件或删失状态、发生事件或删失时间等数据进行汇总，并按时间进行排序，计算公式如下：

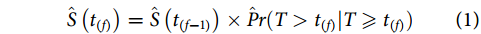基于乘积极限原理（product limit），认为超过某一生存时间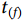研究对象仍存活的生存概率为研究对象在前一时刻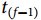仍存活的概率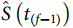与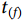时观察人数活过该时刻概率的乘积，从零时刻为1起估计不同生存时间上的生存概率。完成对随访时间内不同生存时间点上生存概率的估计后，即可绘制一横轴为生存时间，纵轴为生存概率的Kaplan-Meier生存曲线图[10]，删失数据可通过曲线上的“+”进行标记。通过绘制Kaplan-Meier曲线，可以直观地了解研究对象各组间生存概率的趋势及比较组间差异。通过Log-Rank检验、Wilcoxen检验、Tarone-Ware检验、Peto检验以及Flemington-Harrington检验等方法[11-15]，可进一步对组间差异进行显著性检验。

Kaplan-Meier方法作为非参数法，使用相对简单，但存在其固有局限，该方法仅能对随访时间内的生存概率进行估计，无法预测研究对象在随访时间外的生存情况。在进行连续型变量间、多组变量间生存概率对比上不够灵活，也无法量化组间不同预后因素对结局的效应。随着研究后期删失数据的增加，Kaplan-Meier方法估计生存概率的准确性也随之下降[16]。

2.2   PH假设下的半参数与参数法

与Kaplan-Meier方法相比，半参数（semi-parametric）法与参数（parametric）法可构建风险函数与生存函数，预测一个或多个变量在不同生存时间对结局的影响，且同时适用于分类变量与连续型变量。

2.2.1   PH假设

处理时间-事件结局数据时，可构建如公式（2）所示风险函数：

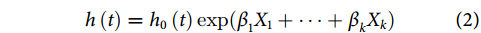为研究对象在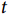时刻发生目标事件的风险，为基线风险函数，其右侧是以多个协变量的线性组合为指数的指数函数，为与研究对象预后相关的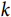个协变量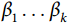，为相应的回归系数。依据公式（2），研究对象中具有不同预后因素个体发生目标事件的风险比（hazard ratio，HR）可表示为公式（3）的形式：

当协变量及其系数不随时间变化而变化时，HR在所有时间点上都保持一个恒定的比例，称为PH[8]。尽管临床研究中也存在协变量和（或）其系数随时间变化的情况，也可对公式（2）进行扩展引入相关的时间函数，但临床研究多是对目前未知的医学现象的探索，由于这一性质，往往不能提前得知协变量及其系数随时间变化的形式并构建准确的时间函数。因此，预后研究中广泛使用基于PH假设的半参数法与参数法。

2.2.2   服从PH假设的半参数法

Cox比例风险回归模型在1972年由David Cox提出[2]，此后成为时间-事件结局数据最为经典的分析方法。在Cox回归模型中，公式（2）中的指数函数为参数部分，而基线风险函数无特定分布，为模型中的非参数部分，因此Cox回归模型被称作半参数方法。同参数法相比，Cox回归模型不要求时间-事件结局数据满足特定的分布类型，在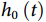无明确定义的情况下也可使用部分似然函数（partial likelihood function）对变量系数进行估计，并且能够得出与基于时间-事件结局真实分布建立的参数模型接近的结果，兼具灵活性及稳健性。在如今尚未有非常精准的方法判定待分析的时间-事件结局服从何种分布的背景下，Cox回归模型成为了预后研究中相对“安全”的选择。值得注意的是，Cox回归模型严格依赖于PH假设，如果在违反PH假设的情况下应用Cox回归模型，模型的统计效能可能会下降。

2.2.3   服从PH假设的参数法

在参数法中，时间-事件结局符合某些特定的分布类型，基于该分布类型可建立回归模型，并使用研究中观察到的数据对模型中未知的参数进行估计。同半参数方法相比，参数法在临床应用中相对局限，但另一方面，在研究者已掌握待分析的时间-事件结局分布的情况下，使用参数法更加的简明，且可构建完整具体的生存函数与风险函数。时间-事件结局中常见的分布类型有Weibull分布、指数分布、Log-Logistic分布、Log-Normal分布以及广义Gamma分布等[17]。在此，williamhill asia 主要介绍服从PH假设情况下常用的指数分布方法与Weibull分布方法。如表1所示，指数分布为单一参数分布，是生存分析中最简单的参数分布形式，其风险函数为一恒定的大于零的常数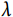，本身即服从PH假设。当构建指数分布模型时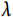，被重参数化，公式（2）可变换为如下形式：

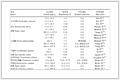表1 指数分布与Weibull分布生存函数与风险函数的形式

表选项

研究者可根据观察的时间-事件数据对模型中的系数进行估计。Weibull分布模型是时间-事件结局分析中最为常用的参数生存模型[18]，其分布涉及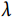与两个大于零的参数。在构建Weibull分布模型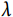，被重参数化，而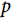保持不变，作为模型中的形状参数（shape parameter），公式（2）可变换为如下形式：

当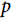>1时，风险函数随时间单调递增，当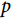<1时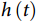，随时间单调递减，而当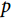为1这一特殊情况时，Weibull分布即退化为了指数分布的形式。同指数分布相比，具有形状参数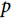的Weibull分布可对风险函数为常数、单调递增、单调递减的情况进行拟合，更加的灵活，也适用于更多的临床场景。

3   时间-事件结局中时间的效应修饰作用及其分析方法

基于PH假设的参数法与半参数法，特别是半参数的Cox比例风险回归模型在预后研究中被广泛使用，但在临床研究中，不服从PH假设的情况时有发生。在近年来兴起的癌症免疫治疗领域，由于药物自身性质或试验设计的影响，治疗药物对目标事件的效应在研究过程中可能出现延后（delayed treatment effect）、随时间削弱（diminishing treatment effect over time）、生存曲线交叉（crossing of hazards）、增强（long-term survivors）等情况[19]。在不服从PH假设的情况下使用Cox回归模型，可能会造成统计效能下降，导致错误的结果。因此，对时间-事件结局数据使用图示法、检验法等方法进行PH假设检验十分重要且必要[20,21]。如图1所示，使用Kaplan-Meier生存曲线对示例数据中心衰住院这一时间-事件结局进行呈现，在未进行PH假设检验的情况下，Log-Rank检验提示两组间存在显著差异（P<0.001），由Cox回归模型计算得出HR为0.71。然而，尽管生存曲线未出现明显不满足PH假设的情况，使用Schoenfeld残差图法进行PH假设检验表明心衰住院结局不符合PH假设（P<0.05，图2）。当数据不服从PH假设时，需要选择其他恰当的方法。

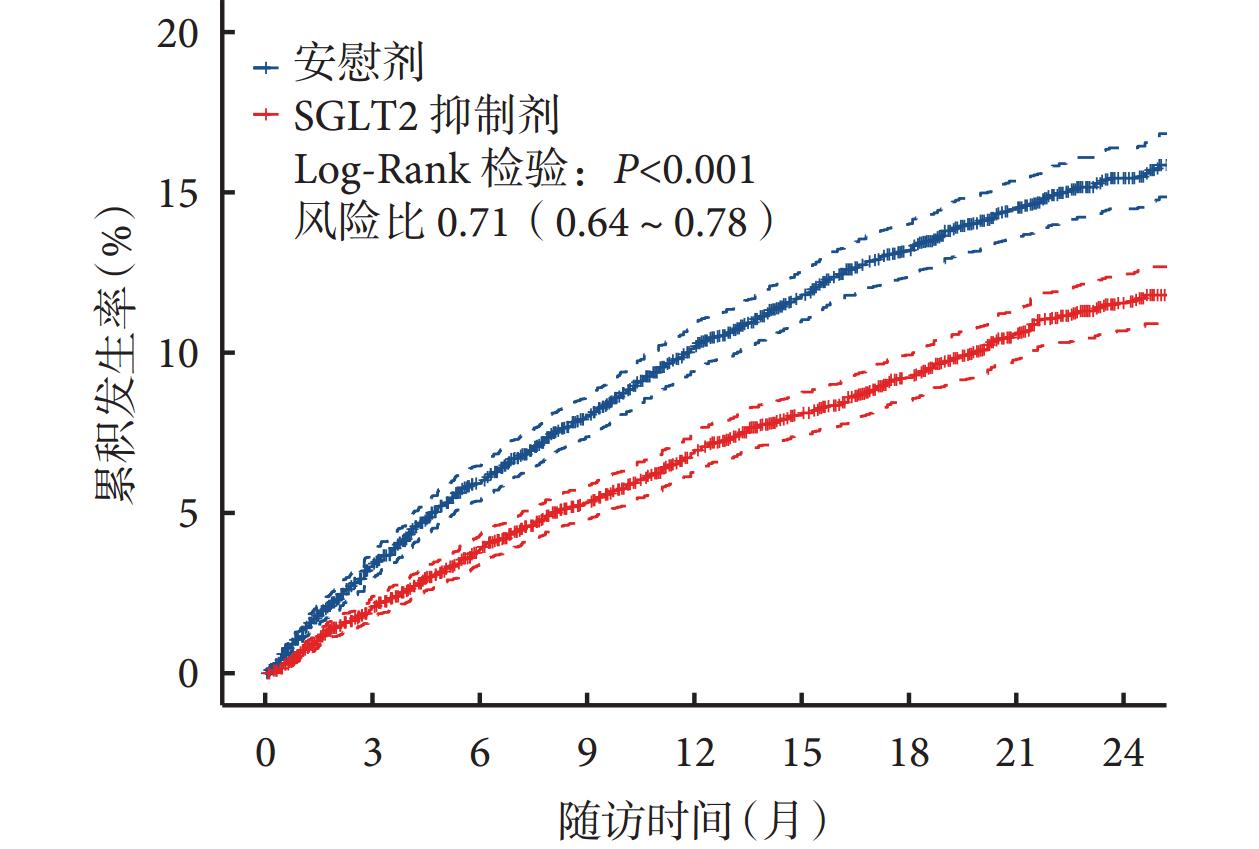图1 Kaplan-Meier生存曲线及Cox比例风险模型结果

图选项

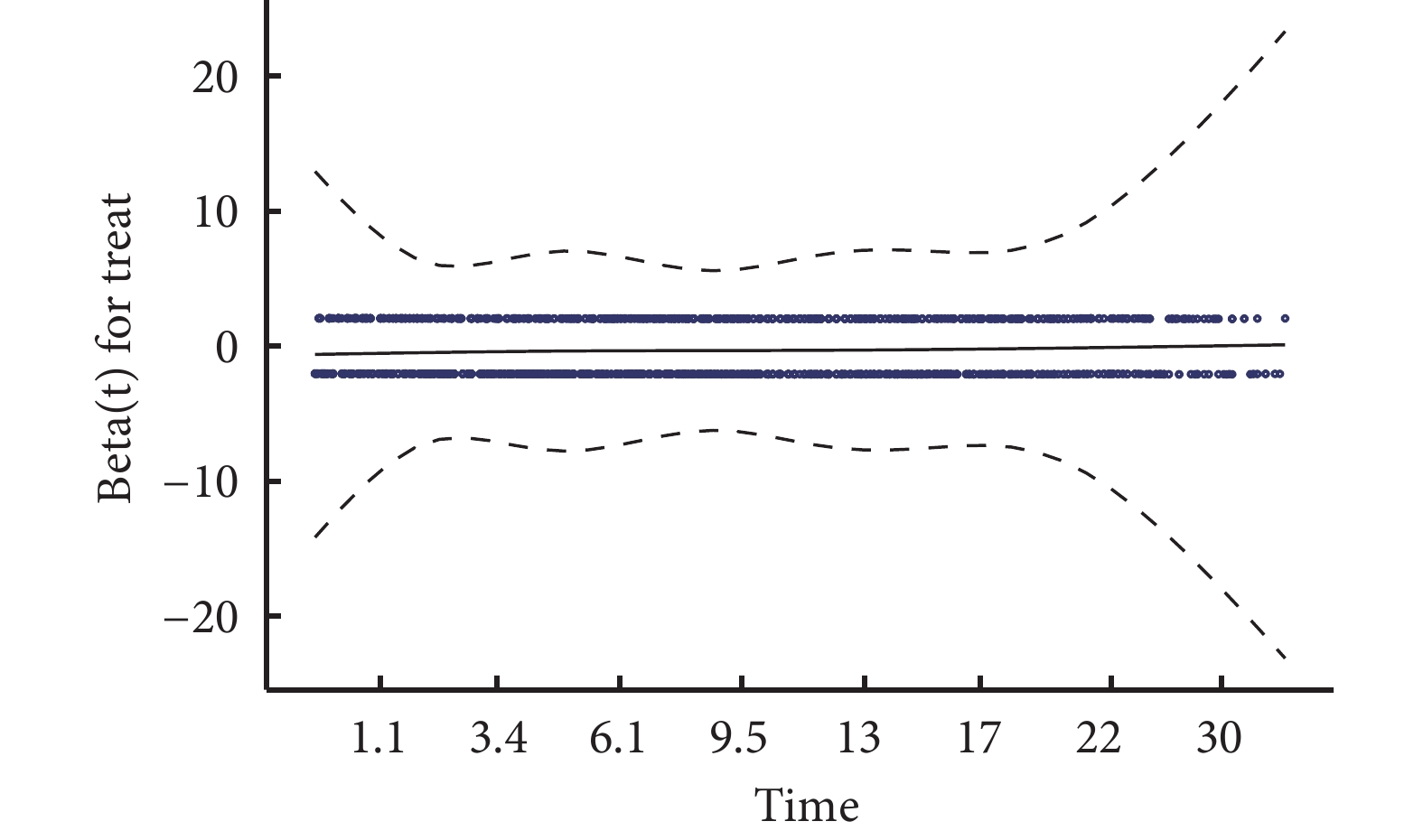图2 Schoenfeld残差散点图

图选项

3.1   时间-事件结局中时间的效应修饰作用

在公式（2）中，当协变量自身的取值保持不变，而其回归系数随时间的变化而变化时，此时的HR不再为一个恒定的值，时间-事件结局不再服从PH假设，协变量对时间-事件结局的效应随时间的变化而变化。这一情况称为时间的效应修饰作用，而随时间的变化而变化的回归系数称为时间依存性系数（time-dependent coefficient），协变量对结局风险的效应称为时间依存性效应（time-dependent effect）[22]。对时间依存性效应常用分析方法见表2。

表2 时间依存性效应常用分析方法的比较

表选项

3.2   界标分析法

Anderson等[23,24]在1983年提出了界标分析法（landmark analysis），最早用于研究肿瘤临床试验中治疗响应（response）与生存结局的关系，处理永恒时间偏倚（immortal time bias）。其基本思想是通过设定一固定的时间点（界标时间），对时间-事件数据进行分段分析，在治疗效应随时间变化时，重点关注所选界标时间后组间生存概率的差异。界标分析法忽略了界标时间之前研究对象发生目标事件、失访等情况，依据该点时研究对象是否接受暴露或产生治疗响应对其进行分组，仅对界标时间后仍然存活并处于随访的研究对象进行生存分析。这一方法的优势在于简单易懂，并可通过Kaplan-Meier生存曲线对界标时间前后的效应进行直观展示。以心衰住院结局为例，选择随访3个月为一界标时间，对生存资料进行分段分析并绘制生存曲线。如图3所示，Log-Rank检验表明，在界标时间前后，SGLT2抑制剂均优于安慰剂。值得注意的是，此处仅是对界标分析法的应用举例，观察图1的生存曲线可知，SGLT2抑制剂对心衰住院的效应并未存在一个明显发生变化的时间点，因此，界标分析法可能不适用处理此类时间依存性效应。而在免疫抑制剂治疗癌症的临床试验中，受试者的长期预后与其对免疫抑制剂的免疫响应有关，在试验前期，大部分受试者未发生免疫响应，试验组与对照组间的结局风险相似，而对试验组中幸存至某一时间点后并发生免疫响应的受试者，其长期预后则可能优于对照组。这类时间依存性效应也反映在生存曲线的“分离晚”或“长拖尾”上，提示治疗效应的延后或增强。在涉及药物支架、主动脉瓣置换术的心血管结局研究中，与接受药物保守治疗的对照组相比，试验组接受创伤性更大的器械辅助治疗的受试者在术后早期的死亡风险较高，而在试验后期，试验组幸存的受试者长期预后则可能更佳。这一在不同时间段相反的治疗效应在生存曲线上则表现为生存曲线的交叉。当涉及癌症免疫治疗、心脏药物支架等可观察到治疗效应变化时间点的研究，或研究者更关心某一时间点的生存结局时，应用界标分析法处理时间依存性效应更加适用[25-29]。但界标分析法有着固有缺陷，其结果的可靠性极大程度上依赖于合理的界标时间选择，如果选择随访时间内靠后的界标时间，则生存分析将排除该点前较多的目标事件，仅纳入少部分尚存的研究对象，使得统计效能和精确性降低，主观的界标时间选择还有得出数据驱动（data-driven）结果的风险。不同的界标时间可能得出不同的结果，使得研究结果间的推广性有限[30]。因此，在使用界标分析法时，应在制定研究计划时即根据临床经验及既往证据选择具有临床意义的界标时间，并在敏感性分析的部分，采取不同的界标时间重复分析以验证结果的稳健性，对界标分析法得出的结果也应谨慎解读。

图3 界标分析法分段生存曲线图

图选项

3.3   限制平均生存时间（restricted mean survival time，RMST）方法

RMST指的是生存曲线在直到某一特定时间的曲线下面积，即该点前研究对象的平均生存时间[31]。RMST方法无需构建特定的模型，不依赖PH假设，通过设置不同的时间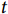，可估计不同时间范围内组间RMST的差值及比值，对治疗效应进行比较[32]。如图4所示，arm=1表示接受SGLT2抑制剂治疗，arm=0表示接受安慰剂治疗，以随访24个月为特定时间点，曲线下蓝色部分面积表示各组RMST，曲线上红色部分面积则表示两组的限制平均损失时间（restricted mean time lost，RMTL），SGLT2抑制剂组与安慰剂组的RMST分别为22.44个月与21.75个月，差异为0.7个月。当生存资料中存在不服从PH假设的情况时，传统生存分析中报告协变量效应的HR变得难以解读，RMST方法不受PH假设限制，还可绘制组间RMST差值随时间变化的趋势图对时间依存性效应进行直观呈现（图5）。这一直接衡量生存时间的指标易于理解，在临床实践中的应用性较强，成为近年来较为常用的替代性结局指标[33-37]。不过RMST方法仍存在一些局限性[38]，目前特定生存时间t的选择尚无公认的最佳方法，研究者应基于临床经验，以Kaplan-Meier生存曲线为辅助，选择恰当的时间点，以展示研究对象在最具有临床意义的时间范围内的生存情况。

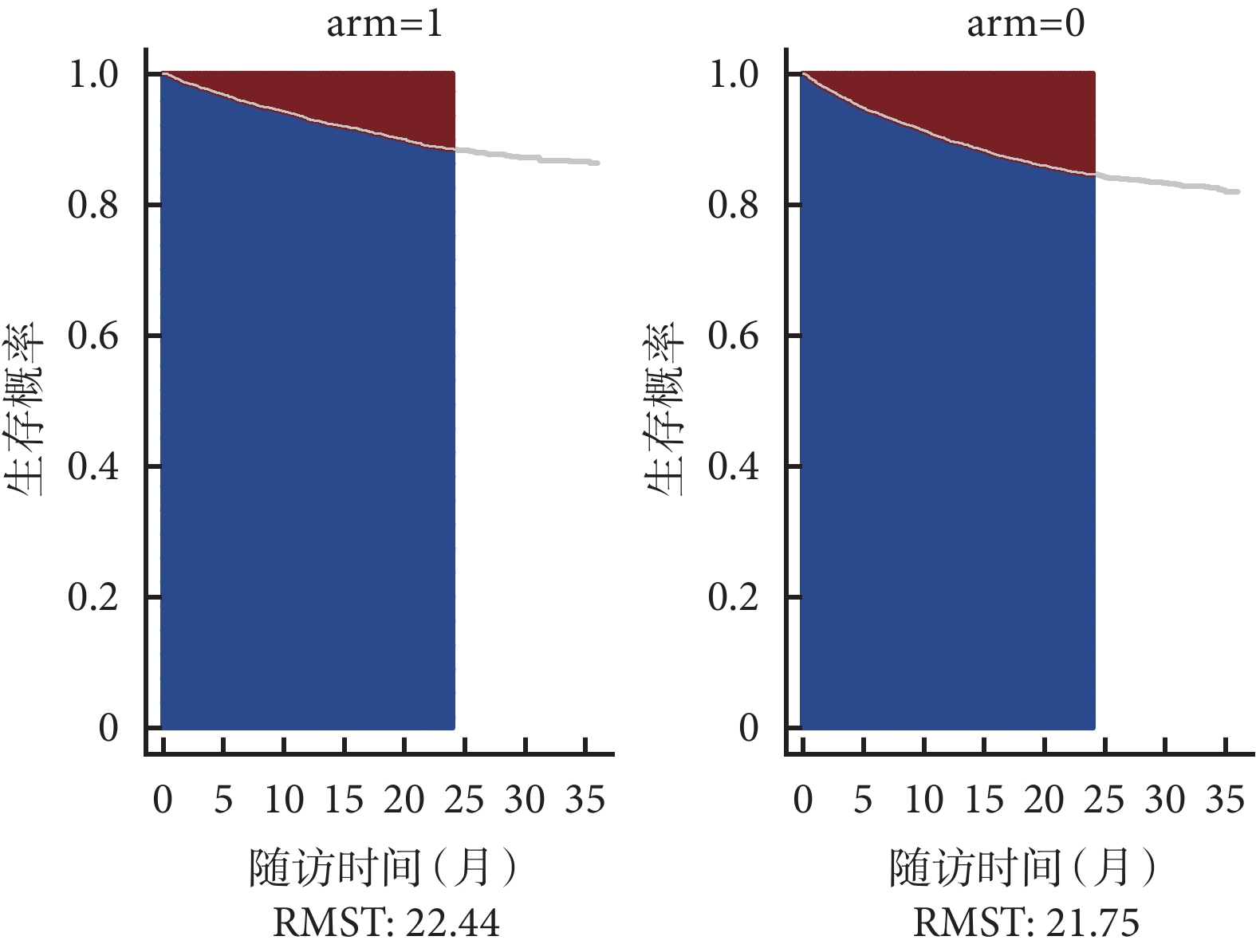图4 SGLT2抑制剂组与安慰剂组限制平均生存时间

图选项

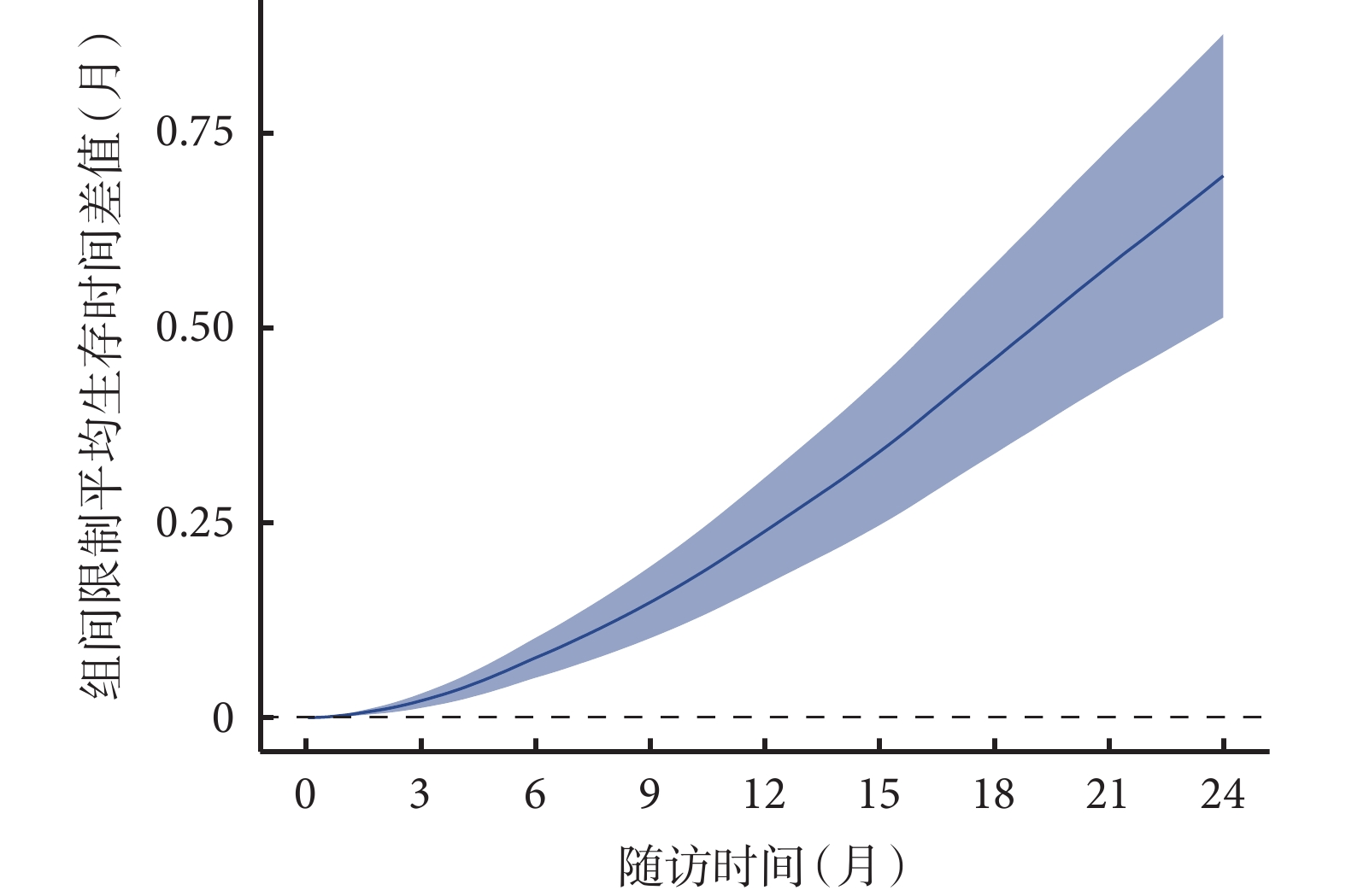图5 SGLT2抑制剂组与安慰剂组限制平均生存时间差值随时间变化的趋势

图选项

3.4   含时间依存性系数的Cox回归模型

当时间-事件结局中存在时间依存性系数时，此时不再服从PH假设，经典的Cox回归模型不再适用。但其可扩展加入时间依存性系数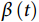，成为：

使用Cox回归模型对时间依存性系数进行处理时，可首先通过图示法了解时间依存性系数随时间变化的趋势，基于系数发生变化的时间拐点对时间-事件结局数据进行分层分析。这种方法较为简单，但却无法估计这一分层的协变量对结局的效应，而当分层较多时，模型的统计效能也将受到影响。当分层分析难以解决问题时，可人为构建一时间依存性协变量（time-dependent covariate），以解决协变量系数随时间变化的问题[8]。时间依存性协变量构建的形式通常根据具体临床问题、数据类型和图示法进行选择，如、、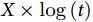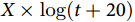等。目前不同选择对结果的影响尚待进一步研究。通过构建含时间依存性系数的Cox回归模型，可以估计出各时间段随时间变化的HR。这些结果可以更为准确地反应效应量的时间依存关系，但其相对复杂的结构对于大多数临床医生而言较为抽象。

3.5   灵活参数生存分析方法

参数法需要以特定的分布为基础建立回归模型，故而在临床应用中受到局限。Royston与Parmar在2002年提出了一种更为灵活的参数模型，即flexible parametric survival model（FPSM）[39]，该方法在Weibull分布、Log-Logistic分布等基础上进行扩展，通过连接函数对生存函数进行转化，借助限制性立方样条函数（restricted cubic spline）平滑基线风险函数，相较于其他参数模型更具灵活性。在生存资料不符合PH假设时，可通过构建时间依存性协变量与基线风险函数相乘交互项，将时间依存性协变量纳入模型进行分析。近年来FPSM法在国外心血管疾病、肿瘤等慢性病研究领域已得到了较多应用，研究者可通过R软件中的“flexsurv”包使用灵活参数生存模型进行分析[40]。

4   时间-事件结局证据合成中时间的效应修饰作用

Meta分析是时间-事件结局数据证据合成中的重要研究方法，能够汇总现有相关临床研究所提供的信息，全面而系统地对干预措施的有效性和安全性进行评价，Meta分析证据也因此被称为临床研究中的最高等级证据。当时间-事件结局中存在可能的时间效应修饰作用时，进行证据合成时也应选择恰当的分析方法。

4.1   基于研究水平报告结果的“两步法”Meta分析

当原始研究报告了时间依存性效应时，williamhill asia 可以基于每个纳入研究研究水平上报告的结果进行效应合并，此即“两步法”（two-stage）Meta分析。然而，不同原始研究可能采取不同的方法对干预措施的时间依存性效应进行估计，即使采取同一方法，方法的实施细节、效应量的报告形式也不尽相同。因此，涉及时间依存性效应时，基于研究水平报告结果的“两步法”Meta分析在效应量的合并上存在挑战，少有报告。

4.2   基于单个患者数据（individual patient data，IPD）的Meta分析

IPD即包含研究对象个体水平协变量特征、生存时间及生存结局的数据。当基于研究水平上报告结果的“两步法”Meta分析难以解决研究问题时，应考虑开展基于原始研究IPD的Meta分析[41]。原始研究的IPD可通过联系相关的研究负责人获取，但这对研究资源的需求大，对研究人员的协调管理能力要求高，通常较难实现。Guyot等[42-44]在2012年提出通过提取Kaplan-Meier生存曲线重建IPD的方法，重建IPD包含了原始研究中个体水平的分组信息、生存时间及生存结局，基于重建IPD也可开展时间-事件结局的Meta分析。

4.2.1   基于IPD的“两步法”Meta分析

当获得原始研究的IPD后，可以开展基于IPD的“两步法”Meta分析，即对不同研究的IPD，使用同一方法（如含时间依存性系数的Cox回归模型）估计不同研究的时间依存性效应，对研究水平的效应量，采取传统Meta分析中加权平均的方法进行效应量的合并。当研究间异质性较大时，可采用随机效应模型进行合并，并进行Meta回归探究异质性的来源[45]。例如，在使用界标分析法时，研究者可对不同原始研究，采取同一界标时间进行分析，再对估计的不同研究间的生存概率、HR等效应量进行合并。含时间依存性系数的Cox回归模型及灵活参数生存模型可估计不同时间范围内的HR，对所关注的具有临床意义的时间范围，研究者可对不同研究间同一时间范围的HR进行合并。使用RMST方法时，可对不同研究选择同一特定时间点，进而对研究水平上RMST的差值或比值进行合并[46]。2021年Weir等开发了基于IPD进行RMST差值“两步法”Meta分析的R软件工具包“metaRMST”，使用者能以曲线图的形式直观展示各个纳入研究在不同时间点的组间RMST差值及其合并后的结果，并可借助灵活参数生存模型、bootstrap等方法实现随访时间外RMST的估计[47]。近年来这一方法在时间-事件结局的Meta分析中也得到较多应用[48-50]。对心衰住院这一结局不同研究的RMST差值进行“两步法”Meta分析，其结果如图6所示，随访3个月与随访24个月时组间RMST差值的合并结果分别为0.02个月与0.68个月。“两步法”Meta分析对不同原始研究的IPD使用同一方法分开分析，再对研究水平的效应量进行合并，除涉及时间的效应修饰作用外，其他部分与常规的Meta分析一致，相对简单易懂。不过，当纳入原始研究随访时间长短不一时，在选择同一时间点进行界标分析法或RMST法时可能存在困难。在部分原始研究删失较多、目标事件数较少的情况下，“两步法”Meta分析的结果也可能存在偏倚。这时，更加适合开展基于IPD的“一步法”（one-stage）Meta分析方法[51]。

图6 SGLT2抑制剂组与安慰剂组限制平均生存时间差值“两步法”Meta分析结果

图选项

4.2.2   基于IPD的“一步法”Meta分析

“一步法”Meta分析方法，是指将不同研究间的IPD进行汇总，使用同一方法对汇总后的IPD进行分析。在“一步法”Meta分析中，使用上述灵活参数生存模型、含时间依存性系数的Cox回归模型等方法对时间依存性效应进行估计时，除考虑研究间的异质性外，还需额外考虑不同研究内的聚类效应（clustering）[52]。处理聚类效应的方法主要有分层分析（stratification）及脆弱模型（frailty model）两种。

分层分析指的是在构建回归模型时对不同研究采取不同的基线风险函数，该方法在纳入原始研究均具有足够的样本量及事件数估计效应量时较为适合，在处理小样本量原始研究时统计效能随之下降。

脆弱模型是处理聚类数据的一种随机效应（random effect）模型[53]，该方法可在基线风险函数中引入脆弱项（frailty terms）这一随机参数（如随机截距），假设该随机参数服从指定的分布，从而允许不同研究在基线风险上存在异质性。在对不同研究的IPD进行“一步法”Meta分析时，指定研究间的随机效应服从Gamma分布或对数正态分布。近年来，基于IPD的“一步法”Meta分析逐渐受到研究者的重视，然而对已发表的文献进行检索后发现，在“一步法”Meta分析中存在忽略聚类效应的情况，使得研究结果的可信度降低。

因此，基于IPD进行“一步法”Meta分析，探究时间-事件结局中时间的效应修饰作用时，需将上述处理时间依存性效应的方法，同处理聚类效应的方法结合起来，才能得出更加准确的结果。这种情况下回归模型的构建较为复杂，得出结果不易解读。随着软件工具的开发，研究者目前可借助R软件中的“mexhaz”包构建包含时间依存性协变量及随机效应的灵活参数生存模型[54]，使数据分析更加高效快捷。以示例数据中心衰住院结局为例，使用“mexhaz”包构建含时间依存性效应、不同研究间随机效应呈对数正态分布的灵活参数生存模型进行“一步法”Meta分析。基于灵活参数生存模型估计不同时间点各组的累积风险并计算出相对危险度，绘制相对危险度随时间变化的曲线图对结果进行可视化。如图7所示，SGLT2抑制剂可减少心衰住院的风险，但其相对效应随时间呈削弱趋势。

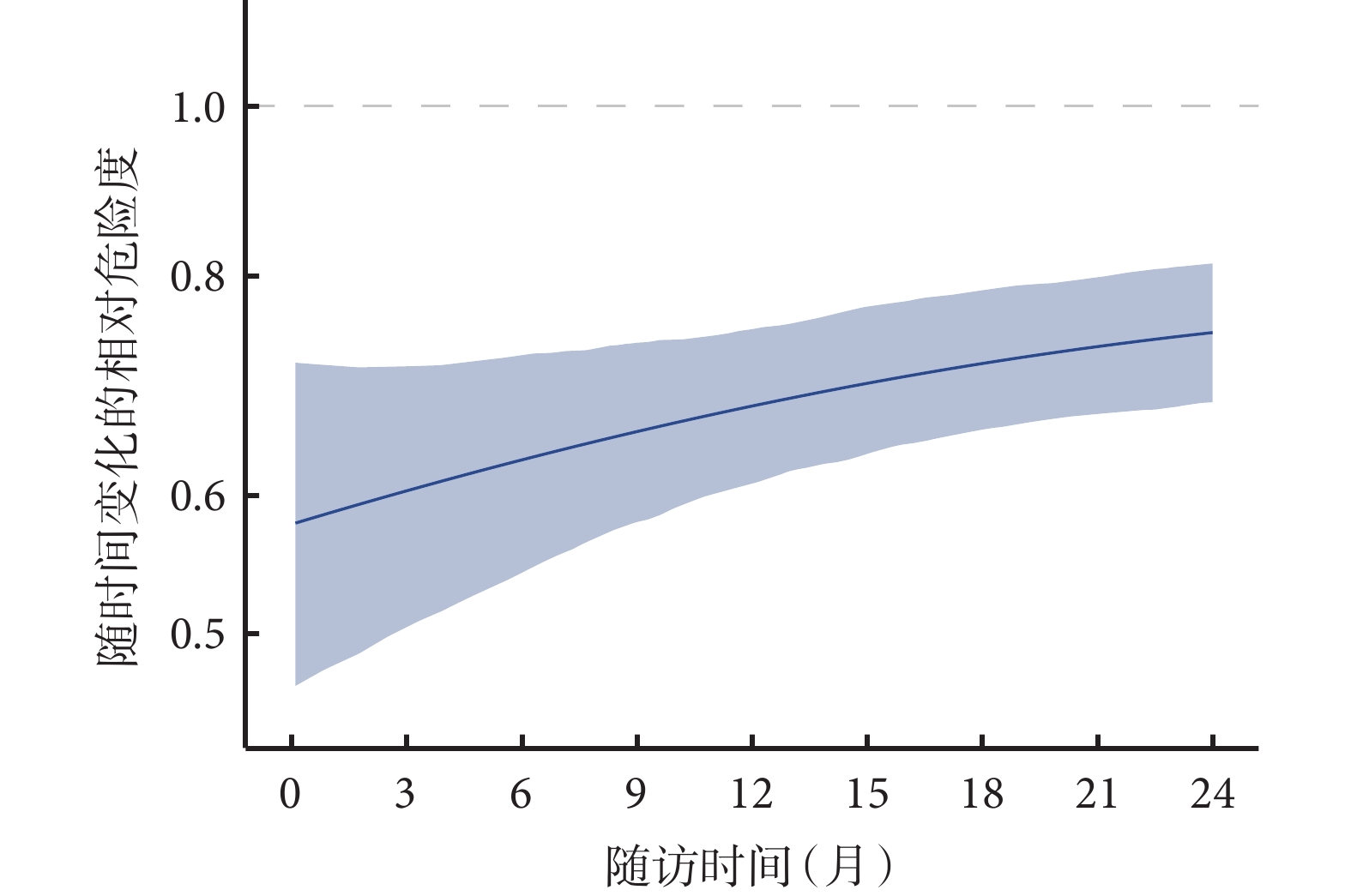图7 心衰住院结局“一步法”Meta分析随时间变化的相对危险度

图选项

5   时间依存性协变量

在时间-事件结局上，不仅存在时间依存性系数，还存在协变量本身随时间变化的情况，这样的协变量称为时间依存性协变量（time-dependent covariate）[8]。时间依存性协变量主要存在3种类型，如3.4所述，第一种是通过设置一个协变量与时间函数的乘积项，在模型中引入时间依存性协变量，属于人为定义的时间依存性协变量，这一时间依存性协变量的引入也适用于解决一些生存资料中协变量随时间变化的情况。例如，在研究药物浓度对生存结局的影响时，可依据药物半衰期，在回归模型中引入协变量与相应时间函数的乘积项进行分析。第二种为内部时间依存性协变量（internal variable），即因为协变量自身性质或个体行为而导致取值随着时间发生变化的协变量。第三种则为辅助时间依存性协变量（ancillary variable），指那些可能因为外部因素变化而变化的协变量，如空气污染指数或就业情况等易受环境或整体经济状况影响的协变量。还有部分兼具内部协变量与辅助协变量性质的协变量，例如临床研究中患者“心脏移植状态”这一协变量，这一取值可能随着随访过程中接受心脏移植而发生变化，而接受心脏移植既受个体健康状态的影响，又受外部医疗资源的影响。除人为定义的时间依存性协变量外，时间依存性协变量在生存资料中通常表现在同一受试者在不同随访时间段记录的某一协变量的不同值。例如，在研究心脏移植手术对心力衰竭患者预后的影响时，可记录到同一受试者在移植前后的数据，在移植前，其“心脏移植”这一协变量取值为“0”，而在移植后，这一协变量取值则为“1”。处理“心脏移植”这一时间依存性协变量，可将同一受试者数据依据移植时间拆分成两条记录，形成新的数据集进行生存分析[8,22]。而对于其他变化形式更为复杂的时间依存性协变量，其分析的难度也随之提高，故在此不做阐述。

6   小结

时间-事件结局中时间的效应修饰作用不可忽视，原始研究的研究者应重视识别时间的效应修饰作用。由于目前处理时间的效应修饰作用的方法各有其优点及局限性，研究者应根据生存资料特点及研究目的选取适合的方法进行分析与报告。在进行时间-事件结局的证据合成时，研究者可借助原始或重建的IPD，进行“一步法”或“两步法”Meta分析处理时间的效应修饰作用。“一步法”与“两步法”均是基于IPD进行Meta分析的重要方法，大部分情况下“两步法”Meta分析即可满足证据合成需求，但在纳入研究受试者及结局事件数较少的情况，“一步法”Meta分析则更加适用，但此时还应注意不同研究间的聚类效应，选择合适的方法进行分析。

原始出处：

邹昕雨, 李舍予. 时间-事件结局证据合成中时间的效应修饰作用. 中国循证医学杂志, 2024, 24(3): 364-372. doi: 10.7507/1672-2531.202310033